Стартовал второй этап нашего конкурса 2023/2024 учебного года!
Конкурс проводится в три этапа: с сентября по декабрь, с января по апрель и с мая по август. Дипломы и призы получат не только победители за весь год, но и победители каждого этапа. Приглашаем всех присоединиться и попробовать свои силы!

Задачи конкурса печатаются в каждом номере. Участвовать можно, начиная с любого тура. Победителей ждут дипломы журнала «Квантик», научно-популярные книги.
Конкурс ориентирован на школьников 5-8 классов, но и младшеклассники могут присылать решения. Вносите решения задач XI тура, с которыми справитесь, не позднее 5 августа в систему проверки konkurs.kvantik.com (инструкция kvantik.com/short/matkonkurs), или высылайте по электронной почте , либо обычной почтой по адресу: 119002, Москва, Б. Власьевский пер., д. 11, журнал «Квантик». В письме кроме имени и фамилии укажите город, школу и класс, в котором вы учитесь, а также обратный адрес.
Задачи и результаты конкурсов прошлых лет: 2022/2023, 2021/2022, 2020/2021, 2019/2020, 2018/2019, 2017/2018, 2016/2017, 2016, 2015, 2014, 2013, 2012.
Желаем успеха!
XI тур
Задача 51. (Татьяна Корчемкина)
Разрежьте фигуру на рисунке по линиям шестиугольной сетки на 6 равных частей.


Задача 52. (Андрей Синюшин)
Коля пришёл в гости к Ване, и приятели решили перекусить. В холодильнике нашёлся кусок сыра такой формы, как на рисунке слева (боковые грани вертикальны и являются прямоугольниками).
Ваня отрезал 4 ломтика толщиной 1 см, как на рисунке справа (это вид сверху). Чтобы всем досталось поровну, себе Ваня собирается взять первый и четвёртый ломтики, а Коле отдать второй и третий. Справедливо ли получится поделить сыр?


Задача 53. (Григорий Гальперин)
У Квантика есть 10 гирь, пронумерованных в порядке возрастания массы, и монетка. Оказалось, что если поставить на правую чашу весов любую гирю с номером больше 1, то для равновесия на левую чашу весов надо положить монетку и все гири с меньшими номерами. Квантик знает, что масса 10-й гири — это 210 = 1024 граммa. Докажите, что тогда и массы остальных гирь, начиная со второй, — тоже степени двойки (то есть 2m граммов для некоторого целого m).

Задача 54. (Дмитрий Калинин)
Фигура «кузнечик» прыгает по доске 4×4, делая ходы по горизонтали или вертикали. Первую клетку кузнечик выбирает по своему усмотрению. Далее он прыгает на соседнюю клетку, потом через одну, потом через две, снова на соседнюю, потом через одну, потом через две клетки и так далее. На каком наибольшем числе клеток может побывать кузнечик, не посещая ни одну клетку дважды?

Задача 55. (Татьяна Казицына)
В комнате находилось несколько человек. Потом в комнату по одному стали заходить ещё люди, первым — Петя, а последним — Вася. После каждого вошедшего средний возраст находящихся в комнате увеличивался на 1 год. Известно, что Пете 26 лет, а возраст Васи в два раза больше, чем количество людей, которое было к моменту его прихода. Сколько людей было в комнате до того, как туда вошёл Петя?

X тур
Задача 46. (Борис Френкин)
У Пети есть картонный прямоугольник. Он хочет разрезать его на части и сложить из них ромб. Помогите ему это сделать.

Задача 47. (Михаил Мурашкин)
Какое из двух чисел, 100! или 100! + 99! + 98!, оканчивается на большее количество нулей? Напомним, что n! — это произведение натуральных чисел от 1 до n.

Задача 48. (Дмитрий Калинин)
На столе лежит стопка блинов. Между соседними блинами либо сметана, либо какая-то одна сладкая начинка — мёд или варенье. Сверху и снизу стопки пусто. У каждого блина ровно одна сторона намазана сметаной. У трети блинов одна сторона намазана вареньем. У 10 блинов одна сторона намазана мёдом. Сколько блинов в стопке?

Задача 49. (Игорь Акулич)
а) Найдите наименьшее целое положительное число, каждая цифра которого равна количеству отличных от неё цифр этого числа.
б) Найдите наибольшее такое число.

Задача 50. (Андрей Бабушкин, 7 класс)
В выпуклом четырёхугольнике ABCD углы A и D равны, AD = AB + DC. Серединный перпендикуляр к отрезку BC пересекает отрезок AD. Докажите, что он делит ABCD на два четырёхугольника одинакового периметра.

IX тур
Задача 41. (Егор Бакаев)
В клетки таблицы 2×50 (состоящей из 50 столбцов по 2 клетки) вписаны 100 различных натуральных чисел. В каждом квадрате 2×2 сумма чисел одна и та же. Могут ли в одном столбце стоять числа 20 и 24?

Задача 42. (Татьяна Казицына)
У Васи живут 5 кошек, каждая либо белая, либо чёрная. За день все кошки вместе съедают ровно один пакет сухого корма. Вася также знает, что любые две кошки разного цвета за день съедят треть пакета корма. Во сколько раз кошки одного цвета съедают больше, чем кошки другого цвета?

Задача 43. (Сергей Полозков)
Музей имеет форму равностороннего треугольника. Директор хочет разделить весь музей на 12 залов в форме равносторонних треугольников (не обязательно одинаковых) так, чтобы можно было начать обход в одном из залов и вернуться в него, пройдя по всем остальным залам и не заходя ни в какой из них дважды (дверь между залами можно установить, только если у них есть общая часть стены). Как это сделать?

Задача 44. (Константин Кноп)
У Кости есть две группы монет, в каждой из которых по одной фальшивой. В первой группе 8 монет, во второй — 10. Фальшивые монеты весят одинаково, чуть легче настоящих. Костя хочет за одно взвешивание на чашечных весах без гирь отыскать больше шести настоящих монет. Получится ли это?

Задача 45. (Никита Солодовников)
Вася построил из картонных кирпичиков 1×2×3 см крепкую стенку 1×200×300 см, потратив целую баночку клея (чтобы стенка была крепкой, любые стороны кирпичей внутри неё должны быть полностью смазаны клеем). Петя сказал, что построил крепкую стенку такого же размера, по-другому располагая такие же кирпичики, и потратил при этом меньше клея. Могло ли такое быть?

VIII тур
Задача 36. (Григорий Гальперин)
Каждый год 1 апреля мистер Х находит сумму цифр своего возраста. В 2024 году эта сумма оказалась в целое число раз больше, чем будет в 2025 году. Сколько лет может быть мистеру Х, если ему больше 1 года, но меньше 100 лет? Укажите все варианты и докажите, что других нет.

Задача 37. (Пётр Хмарук, 5 класс)
Разрежьте фигуру на две равные части:
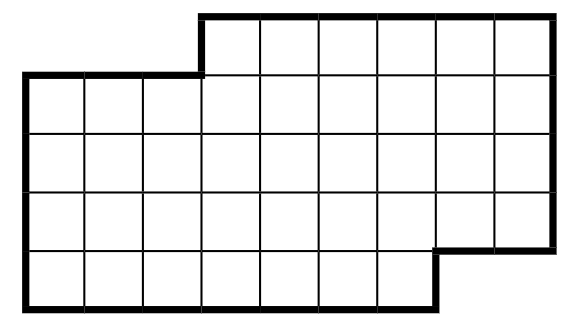

Задача 38. (Алексей Заславский)
Что больше:
1⋅22 + 2⋅21 + 3⋅20 + … + 22⋅1 или 2² + 4² + 6² + … + 22²?
Ответ объясните.

Задача 39. (Григорий Гальперин)
Перед вами карта лабиринта, в который с разных сторон вошли Аня и Ваня. Стена лабиринта — сплошная несамопересекающаяся линия, но часть карты залита чернилами. Пользуясь только этой картой, определите, могли ли Аня и Ваня встретиться в лабиринте, не выходя обратно из своих выходов, или это невозможно?
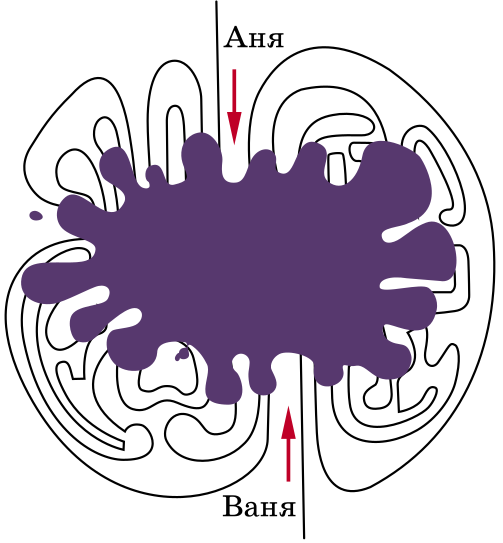

Задача 40. (Георгий Караваев)
Барсуки, белки, бобры и бурундуки встречали Новый год. Сначала все звери, кроме барсуков, водили хоровод, а потом хоровод водили все, кроме белок. В каждом хороводе никакие два одинаковых зверька рядом не стояли. Какое наименьшее количество бобров могло быть на празднике, если белок было на 50 больше, чем барсуков?

VII тур
Задача 31. (Александр Хачатурян)
Маленький Ваня научился писать только две цифры, но смог написать четырёхзначное, трёхзначное и двузначное числа, сумма которых равна 2024. Приведите пример, как это могло получиться.

Задача 32. (Павел Кожевников)
В клетки таблицы 3×3 вписали цифры так, что в каждой строке все 3 цифры разные. Разрешается в каждой строке переставить цифры как угодно. Всегда ли удастся сделать это так, что никакие две одинаковые цифры не окажутся в разных столбцах?

Задача 33. (Павел Кожевников)
Имеется 150 одинаковых плиток в форме равностороннего треугольника. Можно ли из всех этих плиток сложить (без дырок и наложений) какую-нибудь трапецию (то есть, четырёхугольник, у которого две стороны параллельны, а две другие — нет)?

Задача 34. (Михаил Евдокимов)
Коля придумал ребус
КОЛЯ + ВОЛЯ = СИЛА.
Какое наибольшее значение может принимать ИКС? (Одинаковыми буквами обозначены одинаковые цифры, а разными буквами — разные цифры, ни одно число не начинается с нуля).

Задача 35. (Михаил Евдокимов)
Докажите, что для любой пары натуральных чисел m и n найдется клетчатый прямоугольник с соотношением сторон m:n, который можно разрезать на трёхклеточные уголки по линиям сетки так, что уголков каждого из четырёх типов (изображённых на рисунке) будет поровну.


VI тур
Задача 26. (Михаил Евдокимов)
Расставьте на шахматной доске 4×4 четырёх коней и четырёх слонов так, чтобы эти восемь фигур не били друг друга (фигуры бьют друг друга вне зависимости от цвета).

Задача 27. (Борис Френкин)
Гонщик Петя тренируется на кольцевой трассе, длина которой – целое число километров. Он едет 1 км, минуту стоит, едет ещё 2 км, минуту стоит, едет ещё 3 км, минуту стоит, и так далее, пока остановка не совпадёт с начальной точкой, и тогда заканчивает тренировку.
а) Может ли случиться, что Петя не сможет закончить тренировку?
б) Вася тренируется по аналогичной схеме на более короткой кольцевой трассе, длина которой — тоже целое число километров. Могло ли случиться, что они ехали с одинаковой скоростью, но у Пети ушло меньше времени на тренировку, чем у Васи?

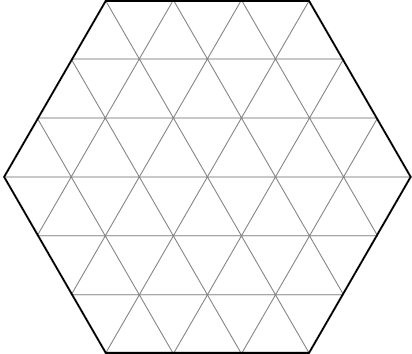
Задача 28. (Татьяна Корчемкина)
Разрежьте шестиугольник на рисунке по линиям сетки на 5 частей одинакового периметра (части могут быть разной формы).

Задача 29. (Николай Авилов)
Индийский школьник Радж закрасил центральную часть таблицы умножения от 1×1 до 19×19 так, как показано на рисунке, и перемножил числа в закрашенных клетках.
А Квантик выписал на доску по разу числа 1 и 19, по 3 раза — числа 2 и 18, по 5 раз — числа 3 и 17, по 7 раз — числа 4 и 16, и так далее, по 17 раз — числа 9 и 11, а число 10 выписал 19 раз, после чего все числа на доске перемножил и возвёл результат в квадрат.
У кого получилось большее число — у Раджа или у Квантика?


Задача 30. (Михаил Евдокимов)
В равностороннем треугольнике ABC отметили точки N, K, M на сторонах AB, BC, AC соответственно так, что AM = 1, BN = 2, BK = 3, CM = 4. Докажите, что треугольник MNK равнобедренный.

V тур
Задача 21. (Михаил Евдокимов)
У Квантика на часах две кнопки: одна выводит на табло дату в формате ДД:ММ, а другая — время в формате ЧЧ:ММ (количество часов принимает значения от 00 до 23). Сколько раз в году Квантик увидит правильное время, даже если перепутает кнопки?

Задача 22. (Егор Бакаев)
Можно ли какой-нибудь пятиугольник разрезать на три равносторонних треугольника (не обязательно равных)?

Задача 23. (Игорь Акулич)
Десятизначное число не содержит нулей и обладает такими свойствами: между любыми двумя единицами (если таковые имеются) расположено не менее одной другой цифры, между любыми двумя двойками (если таковые имеются) расположено не менее двух других цифр, и так далее, вплоть до девяток. Найдите наибольшее и наименьшее числа, удовлетворяющие этим условиям (ответ объясните).

Задача 24. (Егор Бакаев)
Прямоугольник разрезали на четыре треугольника, как схематично показано на рисунке. Оказалось, что закрашенные треугольники равны. Докажите, что тогда и незакрашенные треугольники равны.
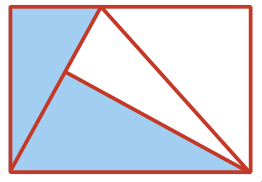

Задача 25. (Сергей Шамсутдинов)
а) Расставьте 12 пешек на доске 6×6, по две на каждой вертикали и на каждой горизонтали так, чтобы никакие две пешки не били друг друга (то есть не стояли на соседних по диагонали клетках).
б) Расставьте 27 пешек на доске 9×9, по три на каждой вертикали и на каждой горизонтали, с выполнением того же условия.

IV тур
Задача 16. (Дмитрий Калинин)
Можно ли записать подряд по возрастанию три последовательных натуральных числа и поставить между ними два знака арифметических действий так, чтобы итог равнялся 2023, если
а) оба раза разрешается использовать любой знак;
б) надо использовать один знак сложения и один знак умножения?

Задача 17. (Татьяна Казицына)
У Пети была кубическая коробка и много кусочков сахара размером 1×2×2. Он смог поместить весь сахар в коробку в несколько слоёв, располагая кусочки параллельно сторонам коробки гранью 2×2 вниз. Потом он решил переложить все кусочки в такую же коробку, располагая их параллельно сторонам коробки гранью 1×2 вниз, но задумался — точно ли это возможно? Помогите Пете ответить на вопрос.

Задача 18. (Сергей Костин)
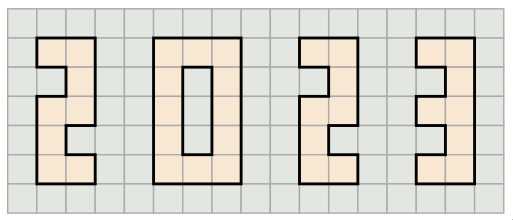
Разрежьте квадрат 6×6 на семь частей и сложите из них изображённую на рисунке фигуру в виде числа 2023.

Задача 19. (Татьяна Казицына)
По кругу стоят 7 диванов, на них сидит всего 50 человек, на каждом диване — хотя бы один человек. Каждый сказал: «На следующем по часовой стрелке диване ровно половина людей выше меня ростом, а ровно половина — ниже». Какое наибольшее число людей могло сказать правду?

Задача 20. (Константин Кноп)
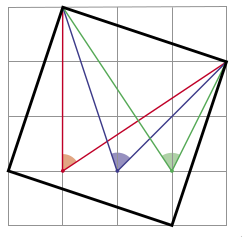
Внутри квадрата со стороной, равной диагонали прямоугольника 1×3 клеточки, отметили три угла — красный, синий и зелёный, — как показано на рисунке. Чему равна их сумма?

III тур
Задача 11. (Сергей Костин)
Число называется палиндромом, если оно одинаково читается слева направо и справа налево (примеры: 7, 77, 787). Представьте число 2023 в виде суммы как можно меньшего количества слагаемых-палиндромов.

Задача 12. (Татьяна Казицына и Борис Френкин)
В полдень из пункта А в пункт Б выехали велосипедисты Алёша и Вася, а навстречу им из пункта Б в пункт А — велосипедисты Боря и Гриша. Каждый ехал с какой-то постоянной скоростью. Спустя какое-то время все четверо одновременно встретились, после чего Алёша и Гриша поехали в пункт А, Боря — в пункт Б, а Вася — в один из этих пунктов, причём он приехал четвёртым (позже всех). Каким по счёту приехал Гриша?

Задача 13. (Александр Грибалко)
Набор состоит из 16 одинаковых фишек в форме равностороннего треугольника. Саша нарисовал на каждой фишке среднюю линию (то есть отрезок, соединяющий середины сторон) и хочет сложить из всех фишек равносторонний треугольник так, чтобы никакие две из этих средних линий не имели общих концов. Сможет ли он это сделать?

Задача 14. (Александр Грибалко)
Перед вами и зрителями выложат несколько монет. Вам по секрету скажут про каждую монету, сколько она весит, а зрителям откроют лишь, что каждая монета весит 2г или 3г, а вместе они весят 23г. Всегда ли вы сможете сделать перед зрителями всего одно взвешивание на чашечных без гирь, после которого они тоже поймут про все монеты, какая сколько весит?

Задача 15. (Илья Сиротовский)
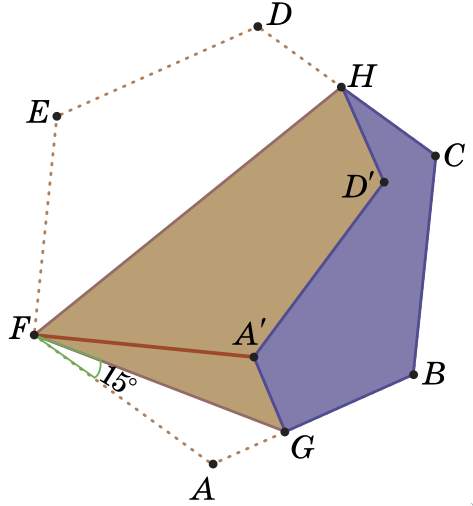
Бумажный шестиугольник ABCDEF, все стороны которого равны 1, а все углы равны 120°, согнули, как показано на рисунке, совместив вершины A и E в точке A´. Угол AFG равен 15°.
а) Найдите периметр шестиугольника HCBGA´D´.
б) Докажите, что точки F, D´, C лежат на одной прямой.

II тур
Задача 6. (Михаил Евдокимов)
Вася заметил, что если записать даты рождения в формате ДД.ММ.ГГГГ, то все цифры на соответствующих местах у него и у его двоюродного брата отличаются. Какова наименьшая возможная разница в возрасте между ними?

Задача 7. (Павел Кожевников)
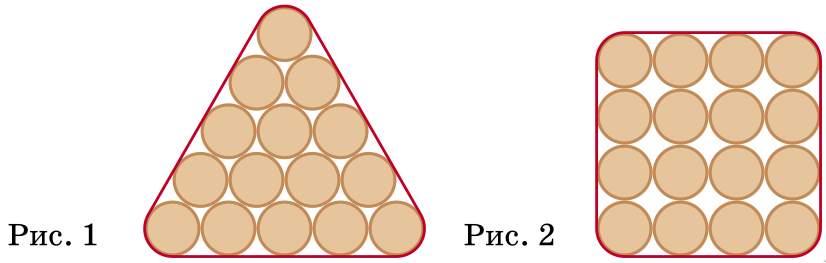
Пятнадцать бочек поставили в виде треугольника (рис.1) и обтянули кольцевым обручем. Шестнадцать бочек поставили в виде квадрата 4×4 (рис.2) и тоже обтянули кольцевым обручем. Сравните длины этих обручей.

Задача 8. (Евгений Смирнов)
Имеются стакан кофе, наполненный на 2/3, и такой же стакан молока, наполненный на 2/3. Разрешается переливать любое количество жидкости туда и обратно, тщательно её перемешивая, но нельзя ничего выливать. Можно ли получить в одном из стаканов напиток, составленный из молока и кофе в пропорции 1:1?

Задача 9. (Татьяна Казицына)
Сделайте на фигуре надрезы так, чтобы полученная фигура не распалась на части и ей можно было обернуть какой-нибудь куб в один слой. (Надрезы нарисуйте сплошными линиями, а сгибы — пунктирными.)
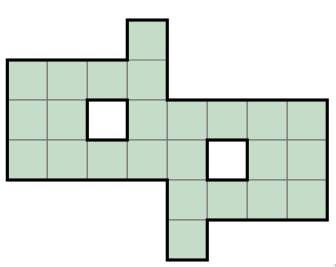

Задача 10. (Сергей Шамсутдинов)
На прямоугольнике 4×8 клеток (половине шахматной доски) разместите трёх ферзей так, чтобы каждое пустое поле бил хотя бы один из ферзей. (Ферзь бьёт по горизонтали, вертикали и диагонали на любое число клеток.)

I тур
Задача 1. (Иван Молодык)
На эскалаторе в метро ступеньки пронумерованы по порядку. На каждой пятой (5, 10, 15, …), на первой и на последней ступеньках краской написаны их номера. Поднимаясь по эскалатору, Вася заметил три подряд идущие ступеньки, на которых были написаны номера. Он сложил эти три номера и получил некоторое число. Назовите последнюю цифру этого числа и объясните, почему она именно такая.

Задача 2. (Михаил Евдокимов)
Разрежьте флажок на две равные по форме и размерам части.
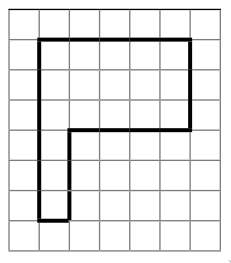

Задача 3. (Татьяна Казицына)
У Вани 4 яблока, у Коли – 41 яблоко, а у всех остальных мальчиков по 14 яблок. Мальчики могут поменяться между собой яблоками так, чтобы у всех стало поровну. Сколько всего мальчиков?

Задача 4. (Александр Грибалко)
У Фелониуса Грю живут 33 миньона, все они весят одинаково. Однажды один из них стащил у Грю банан и съел его, но Грю не знает, кто это сделал. У него есть большие чашечные весы без гирь, на которых он может взвешивать любое количество миньонов. Однако если миньоны оказываются на одной чаше весов, они ссорятся и больше на одну чашу одновременно их ставить нельзя. Как Грю за четыре взвешивания найти воришку, если после съеденного банана он весит больше остальных?

Задача 5. (Михаил Евдокимов)
Каменщик выложил стенку без дырок и полостей из одинаковых кирпичей 1×1×2. Но некоторые кирпичи он положил вдоль, некоторые поперёк, некоторые вертикально, то есть длинное ребро кирпича параллельно одному из трёх направлений. Могло ли оказаться, что кирпичей каждого из трёх типов поровну, если размеры стенки:
а) 3×8×10;
б) 3×9×10?


